The Hamming distance between two strings of bits (binary integers) is the number of corresponding bit positions that differ. This can be found by using $XOR$ on corresponding bits or equivalently, by adding corresponding bits (base $2$) without a carry.

The problem asks for all possible bit strings of length $N$ that are Hamming distance $H$ from the bit string containing all $0$’s (origin).

Consider some random bit string $s$ of length $N$ and a bit string $s^\prime$ of equal length filled with all $0$’s. $XOR$-ing $s$ with $s^\prime$ will leave $s$ unchanged because for single bit $a$, $a \oplus 0 = a$, i.e. the bit is unchanged and this is applicable for all the bits as well. $s \oplus s^\prime$ will have $1$’s in the place where $s$ has $1$’s. The places having bit $1$ indicates that $s$ differs from $s^\prime$ in that position, i.e. $s$ has $1$ in that place and $s^\prime$ has $0$ in that place. A hamming distance $H$ implies that there are exactly $H$ places where $s$ and $s^\prime$ differ and these $H$ places has to have bit $1$.

So the problem asks for all bit strings of length $N$ with exactly $H$ $1$’s printed in ascending lexicographical order.

How many possible bit strings are possible? The string has to be of length $N$, and there has to be $H$ $1$’s. So the remaining $N - H$ bits has to be $0$. How many combinations of $H$ $1$’s and $N - H$ $0$’s are possible? It’s $\displaystyle{N \choose H} = \ddfrac{N!}{H!(N - H)!}$. What is the maximum possible value for this term? $\displaystyle{N \choose H}$ is maximized when the numerator is maximized and the denominator is minimized. The number $N!$ is maximized at $N_{max} = 16$. Then the term becomes a function of $H$, namely $f(H) = \ddfrac{16!}{H!(16 - H)!}$. Let’s look at the graph of $f(H)$:

Graph of $f(H)$

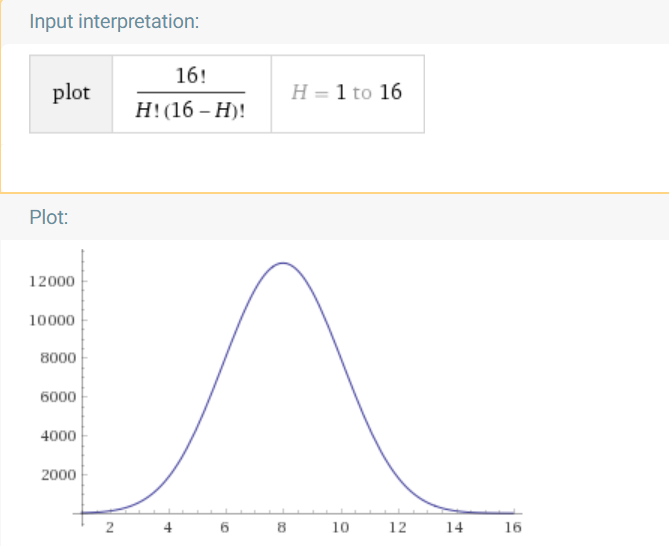
From the graph it’s obvious that $f(H)$ first increases, reached a maximum value at $H = 8$ and then decreases. Also the values seem to be symmetric with respect to $H = 8 = \ddfrac{16}{2} = \ddfrac{N_{max}}{2} $. Why does it behave like this? Please have a look at this post where I’ve discussed in detail about the maximal condition of $\displaystyle{N \choose H}$. The maximum value of ${N \choose H}$ occurs at $\floor{\ddfrac{N}{2}}$ or $\ceil{\ddfrac{N}{2}}$.

As, $N_{max} = 16$ is an even number, $f(H)$ is maximized at $H = \ddfrac{N_{max}}{2} = \ddfrac{16}{2}$ $= 8$ and $f(8) = \ddfrac{16!}{8!~8!} = 12870$.

Now there’s two possible approaches to solving this problem:

  • Generate the lexicographically smallest string containing $H$ $1$’s and then generate the remaining bit strings with backtracking. For example, for $(N, H) = (4,2)$, the lexicographically smallest string of length $4$ with $2$ $1$’s is $s = 0011$. Then we produce the further permutations of this initials string $0101$, $0110$ and so on. There could be duplicate values generated. For example, swapping index $2$ and $3$ of $s$ produces the same string. So we can keep a set to keep track of duplicate values.

Time Complexity: $\mathcal{O}(N!)$ because we need to check all possible permutations starting from the initial string. Given, $N_{max} = 16$, this will not pass the time limit.

  • Iterate all possible $2^N$ bit strings ($2^{16} = 65536$ bits strings in the worst case) starting from bit string with $N$ $0$’s and increase lexicographically. $0000\ldots(N \textrm{zeroes})\ldots0000$, then $0000\ldots(N - 1 \textrm{zeroes}0001)$ and so on. In each iteration, check if the current bit string has $H$ $1$’s. If it has, then print the current bit string and continue. To count how many $1$’s the binary representation of a number has, please refer to this post.

Here’s the implementation in C++:

Time Complexity: $\mathcal{O}(2^N)$ because we need to check all possible $2^N$ bit strings starting from a $N$ length bit strings containing only zeroes. As $N_{max} = 16$, in the worst case we need to check $2^{16} = 65536$ bit strings in the worst case, which is feasible.