This is a graph problem and it can be by Depth First Search (DFS) and recurisve backtracking.
When we normally traverse a graph by DFS, we visit each node, mark it as visited and then visit its neighbors excluding those which have been already visited. We continue traversing until all reachable nodes from the source node has been visited.
This problem asks for all unique walks of length $n$ from the first node. Here unique means for every walk of length $n$, all $n + 1$ nodes are different.
Let’s see an example why straightforward DFS won’t cut for this problem. We’ll use the graph given in the problem statement which corresponds to first sample test case. We’re asked to find all unique walks of length $2$ from the first node.
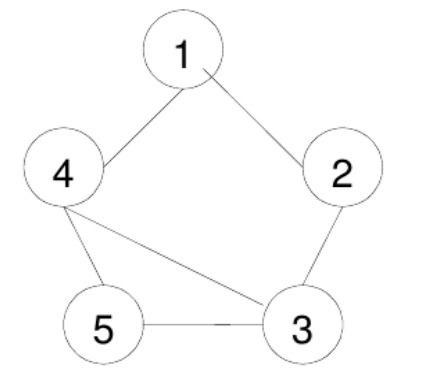
We start from node $1$. When we visit each node, we’ll mark it as visited otherwise we’ll run in a loop and the traversal will continue forever! $1$ has two neighbors - $2$ and $4$. As we have to print the paths in lexicographical (dictionary) order, we’ll first visit $2$ and then $4$. From $2$ we can visit only $3$ as $1$ has already been marked. When we reach $3$, the path length is $2$ which matches with our target length and so we print $\{1,2,3\}$ and return to node $2$. $2$ doesn’t have any more neighbors and we return to $1$.
Now we visit $1$’s next neighbor which is $4$. From $4$ we can go to either $3$ and $5$, but as $3 < 5$ (in dictionary order), we’ll go to $3$ first. But here we run into a problem. $3$ has already been visited! And so we return to $4$. When we reach $5$ from $4$, we print another path $\{1,4,5\}$. We can’t go to any other node from $5$ because the target length has been matched. There’s no other node to visit from $4$ or $1$ and DFS terminates. At the end we have only two walks of length $2$ - $\{1,2,3\}$ and $\{1,4,5\}$. But look at the answer for the first test case. The correct answer is there are three walks of length $2$! We missed $\{1,4,3\}$. What went wrong?
The mistake was to mark $3$ as visited when we were visiting $3$ as $2$’s neighbor. But $3$ is not only $2$’s neighbor but also $4$’s neighbor and depending on other graphs, $3$ can have many other neighbors. So if we mark $3$ as visited when it’s visited from its first neighbor, then the subsequent neighbors will not be able to access $3$. In our case, $4$ was not able to access $3$ when $3$ was visited again (after $2$’s visit).
The solution is to un-mark after it has done visiting all its neighbors respecting the given length constraint. So when we were returning from $3$ (as the target length had already been matched), we should have unmarked it. This is also true for node $2$. If $2$ had an edge with $4$, we would have printed $\{1, 2, 4\}$, but we would have missed $\{1, 4, 2\}$ as $2$ had already been marked. So after a node has done visiting all its neighbors, we have to un-mark it so that it can be accessed as a neighbor from other nodes. This is the notion of recursive backtracking.
Here’s the implementation in C++:
Sharing is caring. Share this story in...
Share: Twitter Facebook LinkedIn