Let’s discuss a problem from 2010 IOI! See the problem at the bottom.
Imagine you’re playing a card game like Concentration. The traditional game is played with two players, but let’s imagine you’re the only one playing.
Suppose, there are a total of $50$ cards and each has exactly one of the letters from $A$ to $Y$ printed on the face, so that each letter appears on exactly two cards. The cards are shuffled into some random order and dealt face down on the table.
You play the game by turning two cards face up so the letters are visible. For each of the $25$ letters you get a candy from your mother the first time you see both copies of the letter on the two face up cards. For example, the first time you turn over both cards that contain the letter $M$, you get a candy. Regardless of whether the letters were equal or not, you then turn both cards face down again. The process is repeated until you receive $25$ candies – one for each letter.
You are to implement a procedure play that plays the game. Your implementation should call the procedure faceup(C) which is implemented by the grader. C is a number between $1$ and $50$ denoting a particular card you wish to be turned face up. The card must not currently be face up. faceup(C) returns the character that is printed on the card C.
After every second call to faceup, the grader automatically turns both cards face down again.
Your procedure play may only terminate once Jack has received all $25$ candies.
Example
The following is one possible sequence of calls your procedure play could make, with explanations.
Call ; Returned value ; Explanation
faceup(1) ; $B$ ; Card $1$ contains $B$.
faceup(7) ; $X$ ; Card $7$ contains $X$. The letters are not equal.
The grader automatically turns cards $1$ and $7$ face down.
faceup(7) ; $X$ ; Card $7$ contains $X$.
faceup(15) ; $O$ ; Card $15$ contains $O$. The letters are not equal.
The grader automatically turns cards $7$ and $15$ face down.
faceup(50) ; $X$ ; Card $50$ contains $X$.
faceup(7) ; $X$ ; Card $7$ contains $X$. You get your first candy.
The grader automatically turns cards $50$ and $7$ face down.
faceup(7) ; $X$ ; Card $7$ contains $X$.
faceup(50) ; $X$ ; Card $50$ contains $X$. Equal letters, but you get no candy because you’ve already seen this pair.
The grader automatically turns cards $7$ and $50$ face down.
faceup(2) ; $B$ ; Card $2$ contains $B$.
…
(some function calls were omitted)
…
faceup(1) ; $B$ ; Card $1$ contains $B$.
faceup(2) ; $B$ ; Card $2$ contains $B$. You get your $25$th candy.
Two subtasks are give. The first subtask asks us to implement any strategy that obeys the rules of the game and finishes it within the given time limit ($2$ seconds).
One simple strategy that can solve the first subtask is the following:
Take the first card. Suppose it contains letter $C$. Now what the maximum number of cards do you need to face up in order to find another card with the letter $C$? It’s $49$, i.e. you would have to look at all the remaining cards. Similarly to find the pair of the second card, we would have to look at $48$ cards in the worst case.
Following the process above, in the worst case we would have to make:
\[2 * (49 + 48 + \ldots + 2 + 1) = 2450 \]
calls to faceup(C). The $2$ at the front specifies that at each step you’re facing up two cards and comparing them. Suppose we always face up the cards on the table from left to right order. So the worst case happens when the first card is paired up with the last card, the second card is paired up with second last card and so on. See the picture below for clarification:
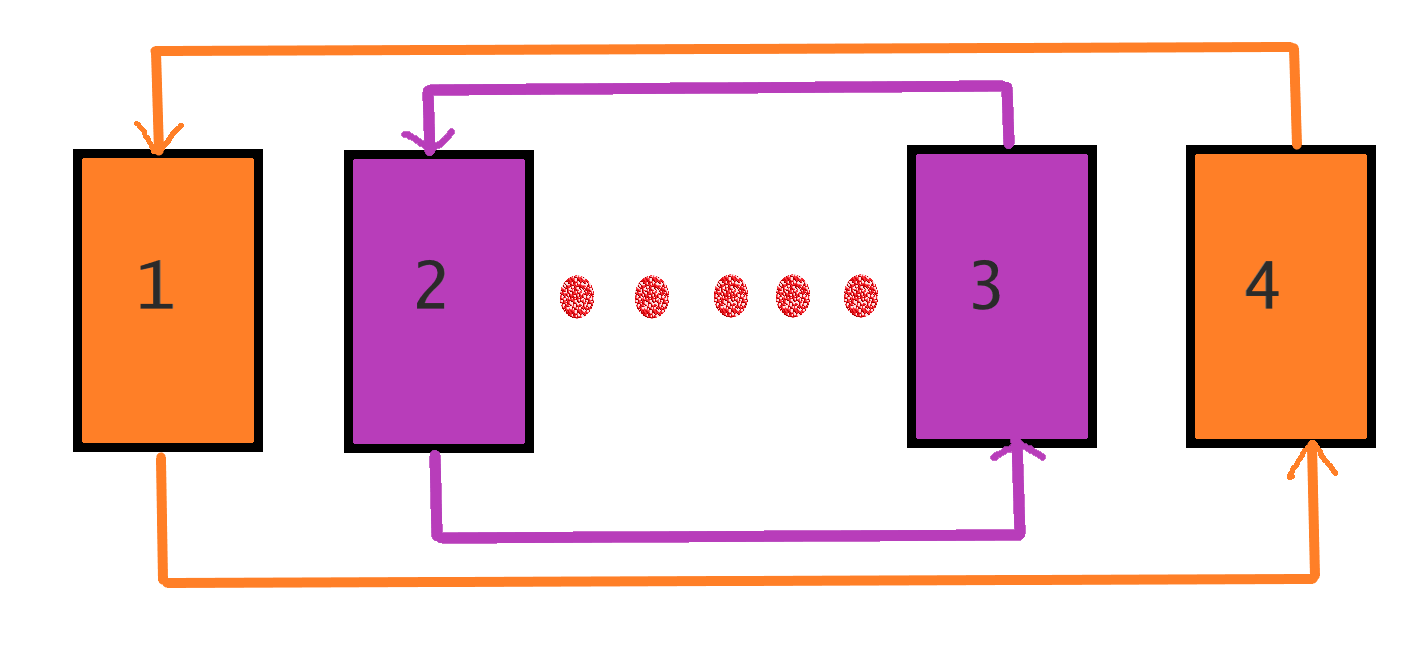
So we’ve established an upper bound and this will pass the time limit for subtask $1$.
For the second subtask, we’re told to come up with a strategy that achieves the objective with at most $100$ faceup function calls!
This sounds like a tough task, but it’s actually not that difficult. First see that, if we somehow knew all the matchings of the cards right from the start (like first card will match with last card and so on), then it would take exactly $50$ calls to faceup to match up all the cards. This is actually a lower bound and we cannot do better than this.
Sadly we don’t know the exact matchings of the card from the beginning. Then we have $100 - 50 = 50$ faceup calls left to figure out the matchings. We can do this by calling faceup(C) for all $1 \leq C \leq 50$. In each call, we’ll get the letter $L$ associated with that card number. We can keep track of the card numbers that are associated with $L$ in a map/dictionary like data structure. As each letter is associated with exactly two numbers, at the end of $50$ calls, we’ll have each letter associated with two numbers. E.g., $[A:\{1,29\}, B:\{2, 37\}, \ldots, Z:\{4, 21\}]$
So after the first $50$ calls we got the mappings of each letter with two card numbers. Then we’ll again call the $50$ cards. At each call, we look up in our map for another card that has the same letter written on it. For example, say we call card $1$ first, and it returns $A$. We look at our map and see that, $A$ is also associated with card $29$. So we call card $29$, and match card $1$ and $29$. We repeat this process for every card. After $50$ calls, all cards will be matched.
In general, if you have $N$ cards, the naive approach takes:
\[ 2 * [(N -1) + (N - 2) + \ldots + 2 + 1] = 2 * \ddfrac{(N - 1) * N}{2} = N * (N - 1)\]
calls in the worst case ($\mathcal{O}(N^2)$ time complexity) and the latter more efficient approach will take at most $2N$ calls in the worst case ($\mathcal{O}(N)$ time complexity).
Problem Link :- Memory - 2010 IOI
Sharing is caring. Share this story in...
Share: Twitter Facebook LinkedIn