Another recursive backtracking problem. Let’s first understand the problem statement.

We’re given an an arithmetic expressing of the following form:

\[ \left(\left(\left(a_{\pi(1)}~o_1~a_{\pi(2)}\right)~o_2~a_{\pi(3)}\right)~o_3~ a_{\pi(4)}\right)~o_4~ a_{\pi(5)}\]

Where $\pi : \{1,2,3,4,5\} \rightarrow \{1,2,3,4,5\}$ is a bijective function and $o_i \in \{+,-,*\} (0 < i < 5)$.

So what is a bijective function? Simply put, it’s a function between the elements of two sets, where each element of one set is paired with exactly one element of the other set, and each element of the other set is paired with exactly one element of the first set. A bijective function is both injective (one-to-one) and surjective (onto). See the following figure:

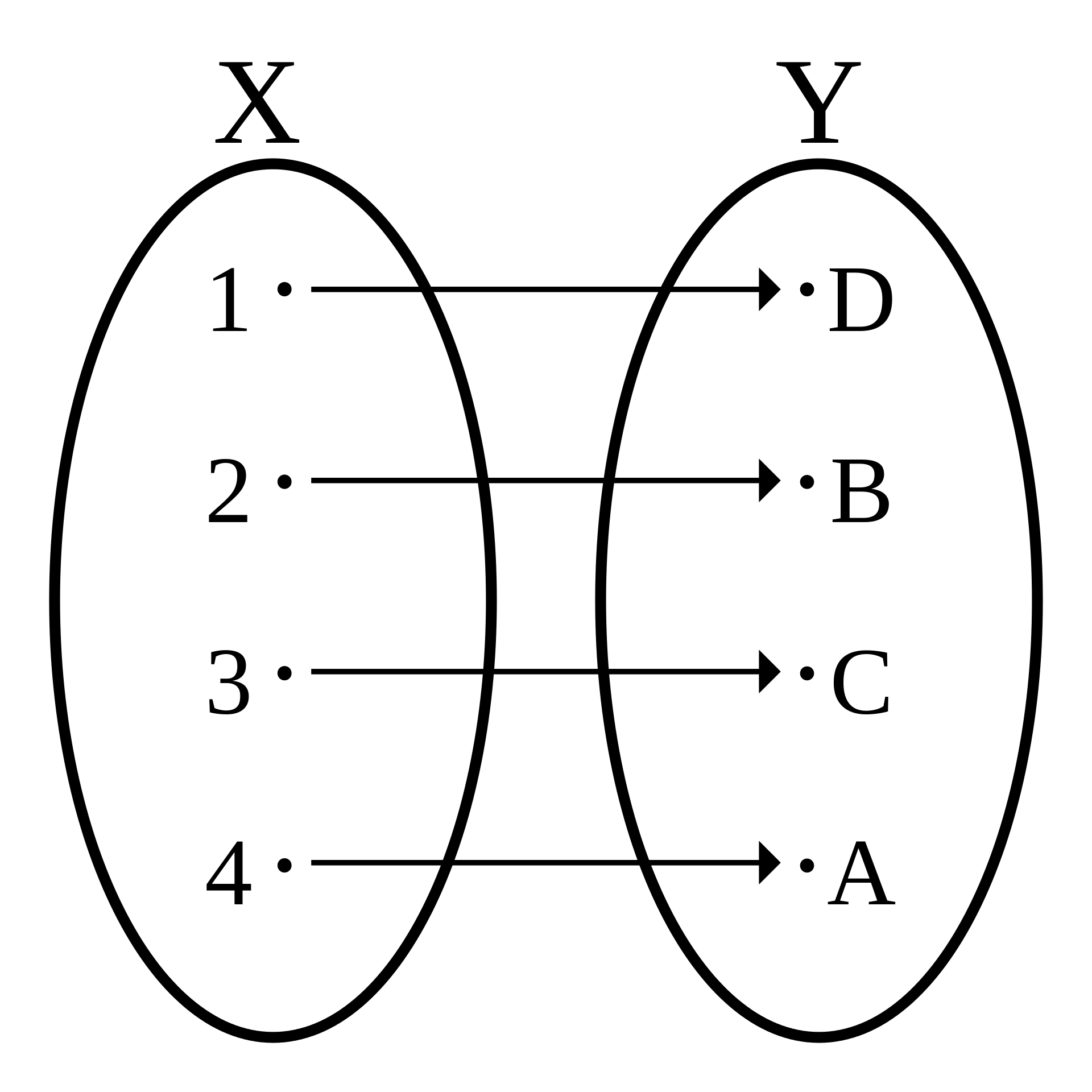
A bijective function, $f: X \rightarrow Y$, where set $X$ is $\\{1, 2, 3, 4\\}$ and set $Y$ is $\\{A, B, C, D\\}$. For example, $f(1) = D$.

In this problem, what it means is that we have to utilize all $5$ numbers and we can utilize it exactly one time. Also notice that the numbers can be placed in any order, and not necessarily in the order they are given. Given that we’re always dealing with $5$ numbers (which have $5$ allocated spaces) and $3$ operators (each of the $3$ operator can sit between any two numbers and we can reuse the operators), in the worst case we have to traverse $5! * 3^4 \approx 10^4$ choices.

Now that we’ve established an upper bound, we can proceed in various ways. First of all, we can generate all the permutations and then place the operators between them. Although it will pass the time limit, this approach is not satisfactory because of two reasons:

  1. If there are duplicates in the origin numbers, this approach will generate duplicate permutations. If all the numbers are same, we actually have one distinct permutation, but this approach will list the same permutation $5! = 120$ times.

  2. It may actually happen that we don’t need to generate all the permutations. We may find a valid permutation long before all of them are enumerated.

We can counteract the first point by keeping the permutations in a set, but it may not reduce the permutations very much, or in other words the number of unique permutations may still be very high.

Another approach is to check the validity of permutation before the next one is generated. This actually has a better run time. For one, it is likely that we don’t have to generate all the permutations because as soon as one solution is found, we can terminate the permutation generation process. Secondly, we can keep track of duplicate permutations by maintaining a set. The permutations which have already been generated and have not yielded a valid result, will not be checked twice.

Let’s see the runtime employing only the first point, i.e. without using set:

Now let’s incorporate set. We’ll first use unordered_set. As unordered_set does not overload the < operator, but vector<int> does, we’ll have to provide a hash function. See this stackoverflow answer and another stackoverflow answer for more details.

See this stackoverflow answer for when we should use unordered_set.

Lastly, we’ll use set:

Although I particularly like this approach, but it doesn’t mean the former two are in any way worse. As the number of permutations is at most $120$, there shouldn’t be any significant performance difference among the three. We don’t have any idea of the test cases, and so blindly saying this is the best may not be the wisest decision. In case of UVa submission, you don’t have any other choice, but if you’re solving real world problem, then you can choose with more freedom as you have access to data and can benchmark various approaches with that data.