This is a very interesting problem. We’re given total volume of the clay used as $V_{total}$ and clay volume consumed in the baking process as $V_0$ ($V_{total}$ and $V_0$ are integers). We’re then asked to compute the number of discs so that the necklace length is longest. Suppose, $n$ discs are used in the process where $ n \in \mathbb{Z} $ (i.e. $n$ is a positive integer). So, the length of the necklace formed by using $n$ discs can be denoted by $f(n)$, where $f(n)$ has the following definition:
\[
f(n) =
\begin{cases}
0.3n\sqrt{\ddfrac{V_{total}}{n} - V_0} & \textrm{if} \quad \ddfrac{V_{total}}{n} > V_0 \
0 & \textrm{if} \quad \ddfrac{V_{total}}{n} \leq V_0
\end{cases}
\]
We have to find out such $n$ so that $f(n)$ is maximized. Futhermore, there are two special cases where we to report $0$ as the answer:
- If no necklaces can be formed at all or
- If the longest length is not unique, i.e. if there are at least two values $n_1$ and $n_2$ such that $f(n_1) = f(n_2)$ and $f(n_1)$ and $f(n_2)$ both are the longest possible necklace length
Regarding the $2$nd constraint, let’s look at the $2$nd sample test case. $V_{total} = 10$ and $V_0 = 2$. Now look what happens when we choose $n = 2$ and $n = 3$:
\begin{aligned}
f(2) = 0.3 * 2 * \sqrt{\ddfrac{10}{2} - 2} = \ddfrac{3\sqrt{3}}{5} \
f(3) = 0.3 * 3 * \sqrt{\ddfrac{10}{3} - 2} = \ddfrac{3\sqrt{3}}{5}
\end{aligned}
So we wound up exactly the same result (and in this case, this is the longest necklace length possible for integer $n$) for two different values of $n$. So, the answer is $0$ for the second sample test case.
Now that the problem statement is out of our way, let’s see how we can approach this problem. As we have to maximize a function, it’s always helpful to look at some graphs. Let’s look at the graph for the first sample test case:
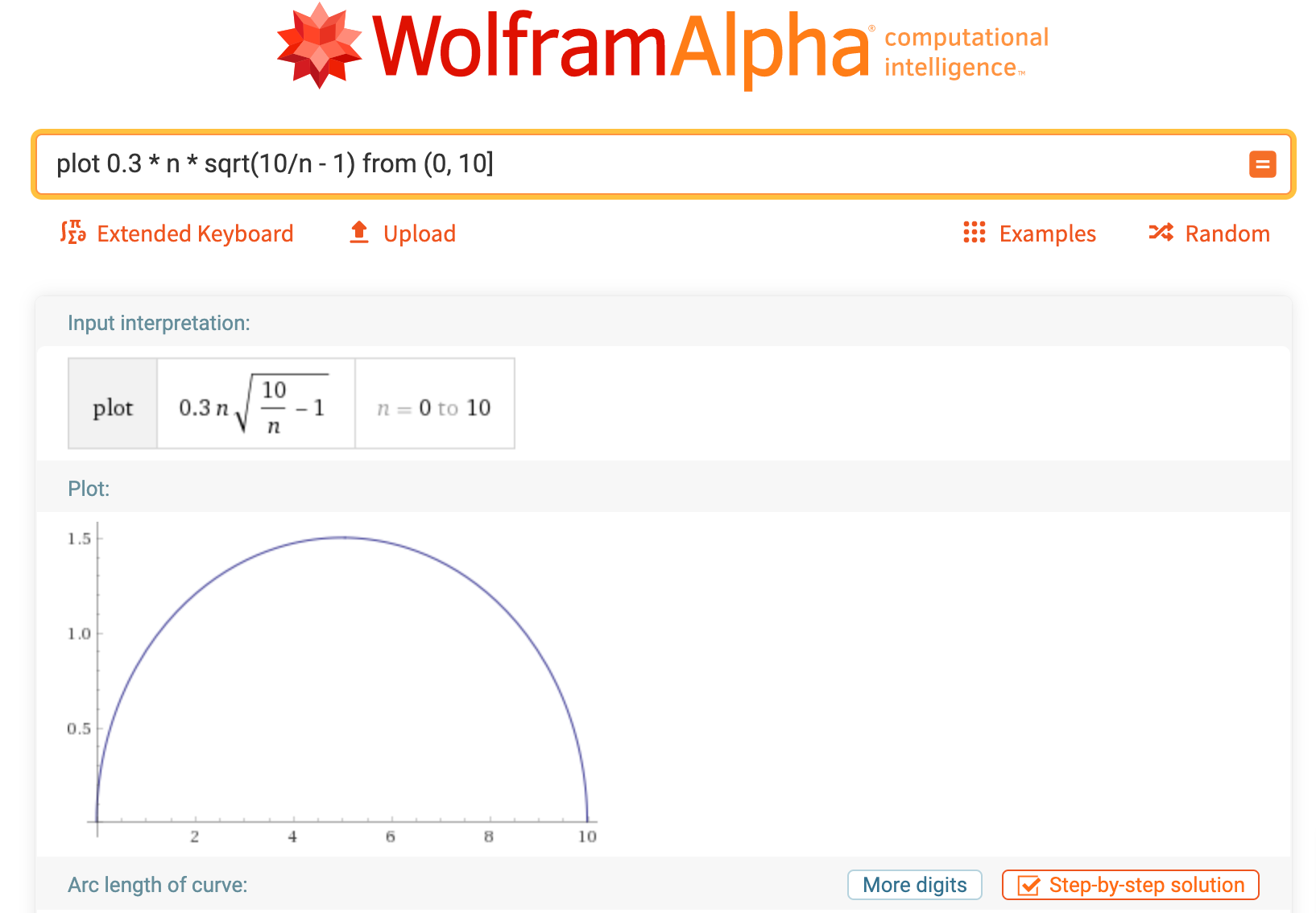
Why did we graph up to $n = 10$? Because if $n > 10$ then $\ddfrac{V_{total}}{n} = \ddfrac{10}{n > 10} = 0$ according to the function definition.
Let’s take another look at the function definition. The first condition tells us that,
\begin{aligned}
\ddfrac{V_{total}}{n} > V_0 \
\implies \ddfrac{n}{V_{total}} < \ddfrac{1}{V_0} \
\implies n < \ddfrac{V_{total}}{V_0}
\end{aligned}
We have an upper bound on $n$, i.e. $n_{max} < \ddfrac{V_{total}}{V_0}$ . Also we have a lower bound as well. As $n$ is a positive integer, $n_{min} = 1$.
Now that we have a lower and an upper bound, can we just just enumerate all possible values to see which one gives the longest necklace length? Well, let’s look at the constraints:
- $0 < V_{total} \leq 60000$ and
- $0 < V_0 \leq 600$
So if we start enumerating all $n$ values starting from $1$, what is the maximum possible $n$ value that we have to enumerate? In the worst case, $n$ is as high as possible. As upper bound of $n$ is defined in terms of $V_{total}$ and $V_0$, we have to take highest value of $V_{total}$ and lowest value of $V_0$ to maximize upper bound of $n$. We have, $V_{total_{max}} = 60000$ and $V_{0_{min}} = 1$ and that makes $n < \ddfrac{60000}{1} = 60000$. So in the worst case we have to enumerate from $n = 1$ to $n = 60000$. That’s doable!
Now that we have a feasible approach, there are still one question that need to be answered:
- How do we know if there are multiple integer $n$ values which yield longest necklace length?
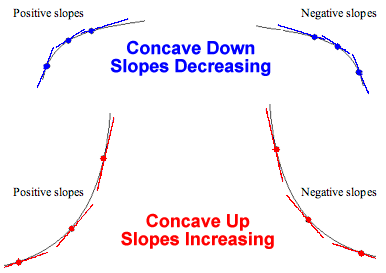
This is where the graph will come in handy! Look at the shape of the graph. It’s concave downward, meaning the slope of $f(n)$, i.e $f^\prime(n)$, is decreasing with increasing $n$. See the following figure for more clarification:
In our case:
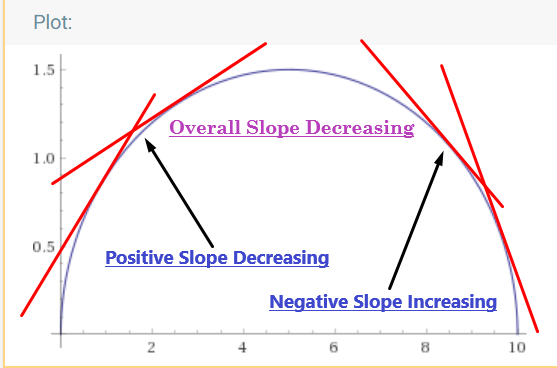
From the graph, it’s obvious that the function $f(n)$ has a global maxima and no local maxima. But we can’t tell if the global maxima is unique or not. One way to determine the $n$ values for which $f(n)$ is maximized is to differentiate $f(n)$ and set it to $0$. Namely, solve the following equation:
\[f^\prime(n) = 0 \]
Let’s first differentiate $f(n)$:
\begin{eqnarray}
f(n) & = & 0.3n\sqrt{\ddfrac{V_{total}}{n} - V_0} \nonumber \
\implies f^\prime(n) & = & 0.3 \left[\sqrt{\ddfrac{V_{total}}{n} - V_0} - \ddfrac{V_0}{2n\sqrt{\ddfrac{V_{total}}{n} - V_0}} \right] \nonumber \
& = & 0.3 \left[\ddfrac{V_t - 2nV_0}{2n\sqrt{\ddfrac{V_{total}}{n} - V_0}}\right] \nonumber
\end{eqnarray}
Now setting $f^\prime(n) = 0$ yields:
\begin{eqnarray} \label{uva-11001-eqn1} \ddfrac{V_t - 2nV_0}{2n\sqrt{\ddfrac{V_{total}}{n} - V_0}} = 0 \end{eqnarray}
\eqref{uva-11001-eqn1} is $0$ whenever the numerator is $0$. Setting the numerator in \eqref{uva-11001-eqn1} to $0$ yields:
\begin{eqnarray}
V_t - 2nV_0 & = & 0 \nonumber \
\label{uva-11001-eqn2}
\implies n_{max} & = & \ddfrac{V_t}{2V_0}
\end{eqnarray}
From differentiating $f(n)$, we found out two important things:
- the $n$ value for which $f(n)$ is maximized
- The global maxima is unique as the numerator in $f^\prime(n)$ is linear in terms of $n$. Namely there’s no two (or more) $n$ values for which $f(n)$ is maximized.
It is also useful to look at $f^{\prime\prime}(n)$, i.e. the second derivate of $f(n)$:
\[ f^{\prime\prime}(n) = -\ddfrac{V_{total}}{4n^3\left(\sqrt{\ddfrac{V_{total}}{n} - V_0}\right)^{3/2}} \]
As the numerator is never zero in $f^{\prime\prime}(n)$, $f^{\prime\prime}(n)$ is always negative in the range $\left(0, \ddfrac{V_{total}}{n} \right)$. As second derivate is always negative, it implies that that $f(n)$ is strictly concave upward, i.e. $f^\prime(n)$ is strictly decreasing.
- $f(n)$ has no two (or more) equal values before the global maximum is reached. Why is this true? Suppose we have two $n$ values as $n_1$ and $n_2$ ($n_1 \not= n_2$ and $n_1 < n_2 < n_{max}$). Then we have $f^\prime(n_1) > f^\prime(n_2)$ as the positives slopes are strictly decreasing in the range $\left(0, \ddfrac{V_{total}}{2V_0} \right)$. This implies, $f(n_1) > f(n_2)$.
- After the global maximum is reached, $f(n)$ value starts decreasing. Similar to the point above, there’s no two (or more) equal values of $f(n)$ in the range $\left(\ddfrac{V_{total}}{2V_0}, \ddfrac{V_{total}}{V_0}\right)$
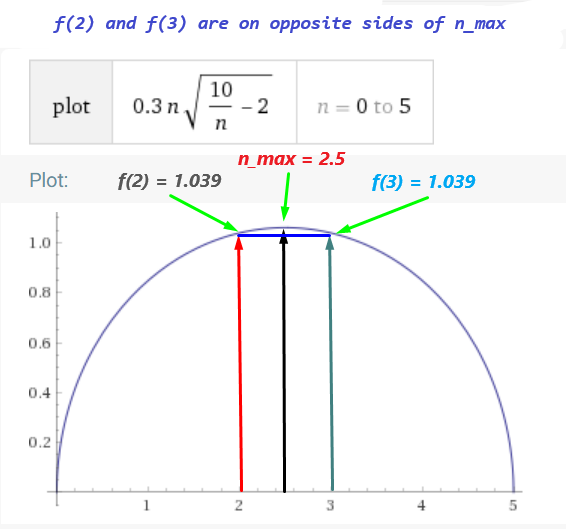
- Taking the previous two points into consideration, we can conclude that if $f(n)$ has two (or more) equal values in the range $\left(0, \ddfrac{V_{total}}{V_0} \right)$, then they must be opposite sides of the global maxima. See the picture below for more clarification:
$n_{max}$ can be an integer or a fraction. But we’re only interested in integer values. If $n_{max}$ is an integer, then we’re done because no other integer values of $n$ will produce the longest necklace length (global maxima is unique).
But what will we do if $n_{max}$ turns out to be a fraction? We’ll take the floor and ceil of $n_{max}$ and compute necklace length for these two values. If they’re equal, then report $0$ as the answer. Otherwise, report the one that gives the longest necklace length. Why only floor and ceil? Because no other integer values of $n$ will produce the longest necklace length (as the slopes are strictly decreasing).
Here’s the implementation in C++:
Time Complexity: $\mathcal{O}(1)$
Sidenote: There’s also an $\mathcal{O}(n)$ solution for this problem. This is basically what we thought as our first approach, i.e. to enumerate all $n$ values. In this approach, we compute necklace length for increasing $n$ values and update the maximum necklace length as we move forward. We break out of loop if one the following conditions are fulfilled:
- If some $n$ value is reaches such that $\ddfrac{V_{total}}{n} \leq V_0$
- As further $n$ values will result in $0$ necklace length
- If the maximum necklace length is equal to the current necklace length (computed for some $n < \ddfrac{V_{total}}{V_0}$
- This will only happen if $n_{max}$ is a faction. When this happens, maximum necklace length is updated for $n^\prime < n_{max}$, and the next integer after $n_{max}$ produces the same result, i.e. $f(n^\prime + 1) = f(n^\prime)$. So, we can just break out of loop here as no further values of $n$ will produce longer necklace length (slopes are strictly decreasing).
Here’s the implementation in C++:
Time Complexity: $\mathcal{O}(n)$
Sharing is caring. Share this story in...
Share: Twitter Facebook LinkedIn