An important observation is that if you have two pieces as $MF$ and $FM$, then you could piece them together to form a loop. See the picture below for clarification:

MF and FM combination

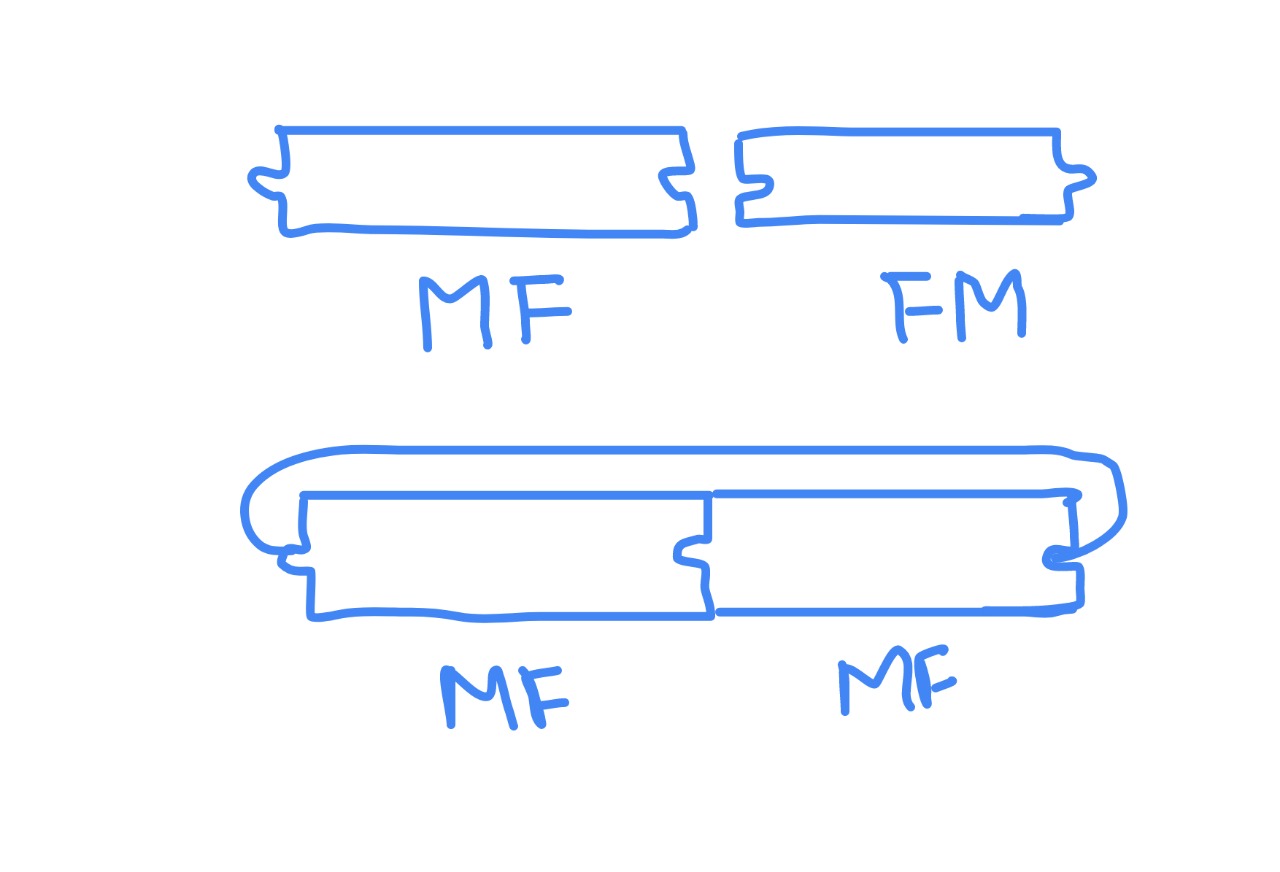
But if we had only one $MF$ or only one $FM$, then a loop couldn’t be formed because the problem states that: “You may not connect the two ends of the same piece together.”

Now, here comes another interesting observation. We’ve just seen from the above example that $MF$ and $FM$ pieces are basically the same. So, if we have more than one $MF$ or $FM$, then a loop can always be formed with them!

Multiple MF combination

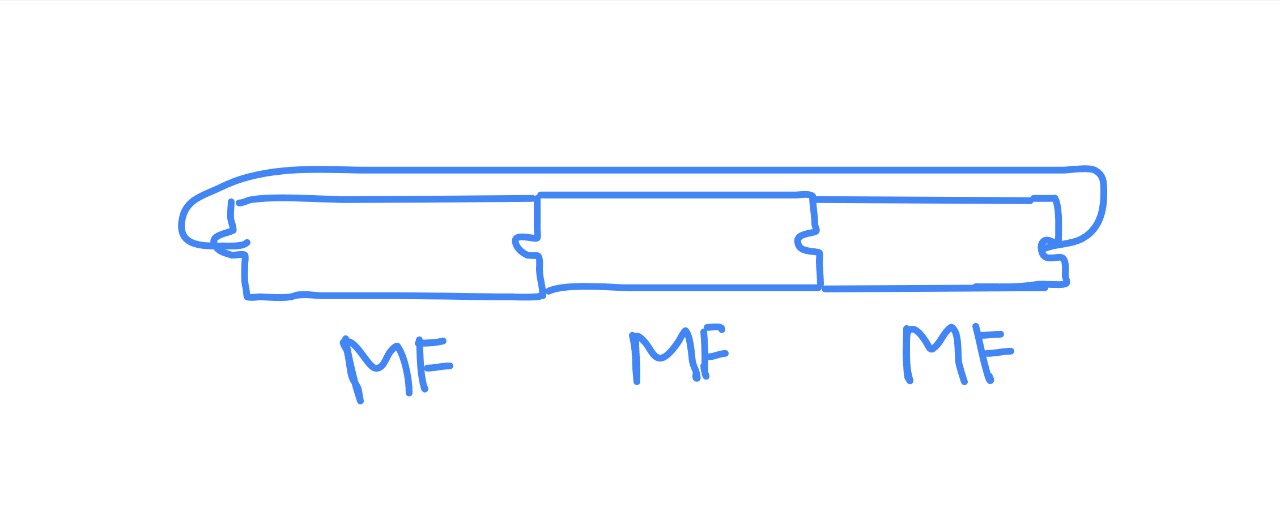
Now comes the $MM$ or $F$ pieces. Observe that, to form a loop, a $MM$ piece must always be accompanied by a $FF$ piece. No matter how many $MF$ or $FM$ pieces there are, if there aren’t equal number of $MM$ and $FF$ pieces (same parity), a loop can’t be formed.

With all that in mind, here’s my implementation in C++: